Desenhando Curvas - I
Agora que já sabemos desenhar um polígonos com begin_shape() e end_shape() ou end_shape(CLOSE) podemos experimentar formas curvas no py5, primeiro curvas Bézier cúbicas, com as funções bezier_vertex(), em seguida curvas Bézier quadráticas usando quadratic_vertex() e por fim uma implementação de Catmull-Rom splines com curve_vertex().
As curvas Bézier levam o nome do engenheiro francês Pierre Bézier, que as desenvolveu a partir dos algorítimos do matemático e físico francês Paul de Casteljau, em seus trabalhos na década de 1960 na indústria automotiva. As curvas Bézier descrevem formas a partir das coordenadas de pontos, ou âncoras, que delimitam o início e o fim de um trecho de curva, mas também precisam de coordenadas de “pontos de controle” que em geral ficam fora da curva, alterando o seu comportamento. Essas curvas polinomiais podem ser expressas como a interpolação linear entre alguns pontos como descrito e ilustrado com animações na Wikipedia.
Curvas Bézier cúbicas com bezier_vertex()
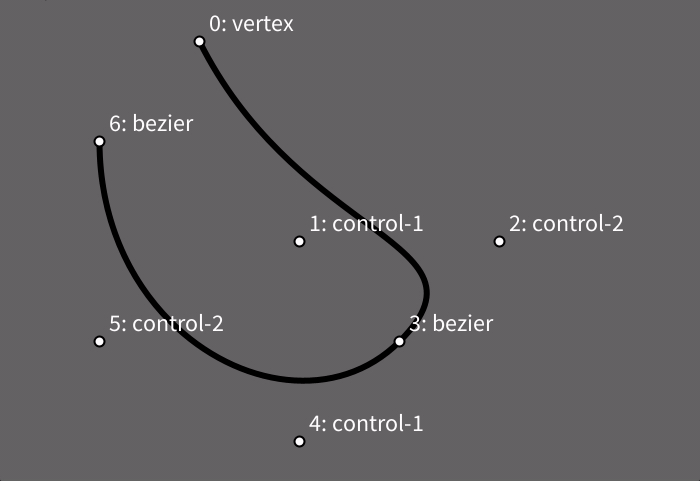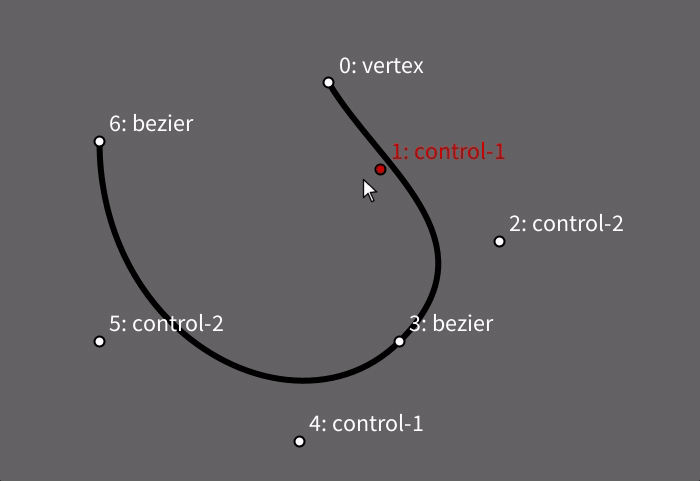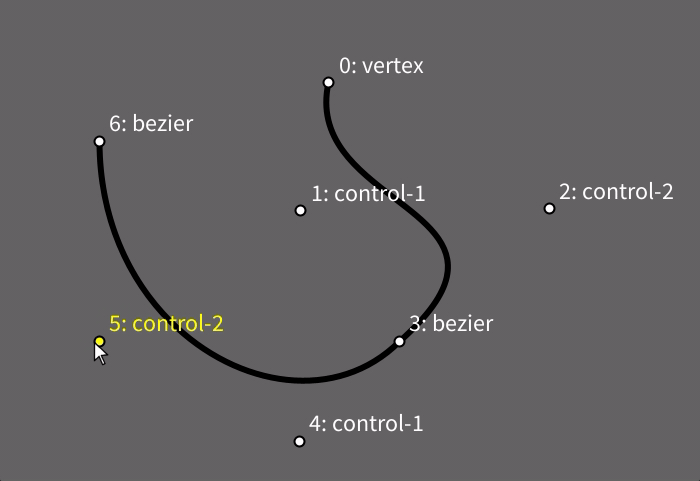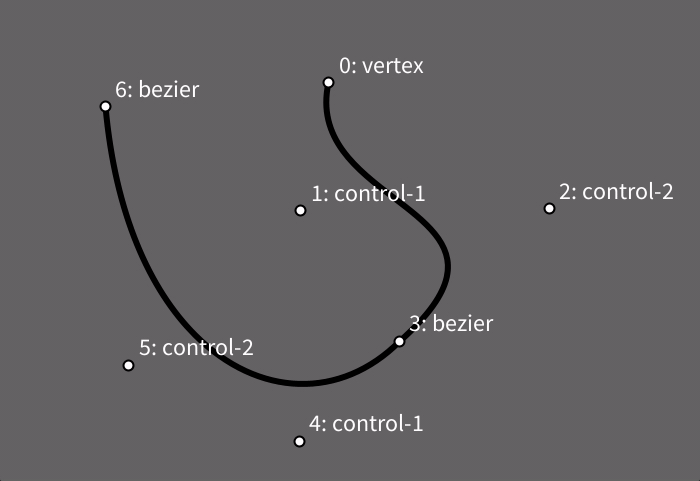
Podemos criar uma forma curva aberta com uma ou mais chamadas a bezier_vertex() entre o begin_shape() e o end_shape(). A curva pode ser fechada se usarmos end_shape(CLOSE) ao final.
Note que antes de cada bezier_vertex() é preciso que haja algum vértice, um ponto âncora, então, antes da primeira chamada a bezier_vertex() em geral é usada uma chamada da função vertex(), como neste exemplo a seguir. Este primeiro tipo de curva Bézier que veremos requer dois pontos de controle para cada novo vértice, sem levar em conta o primeiro vértice-âncora, por isso, na função bezier_vertex() os quatro primeiros argumentos são as cordenadas de dois pontos de controle e os últimos dois são as coordenadas do vértice. Cada vértice Bézier por sua vez pode servir de âncora para um próximo vértice Bézier, permitindo o encadeamento de trechos curvos.
size(400, 300)
begin_shape()
vertex(100, 50) # 0: âncora inicial
bezier_vertex(150, 150, # 1: primeiro ponto de controle do primeiro vértice
250, 150, # 2: segundo ponto de controle do primeiro vértice
200, 200), # 3: vértice final da primeira curva, âncora da segunda
bezier_vertex(150, 250, # 4: primeiro ponto de controle do segundo vértice
50, 200, # 5: segundo ponto de controle do segundo vértice
50, 100) # 6: segundo vértice bezier (final)
end_shape()
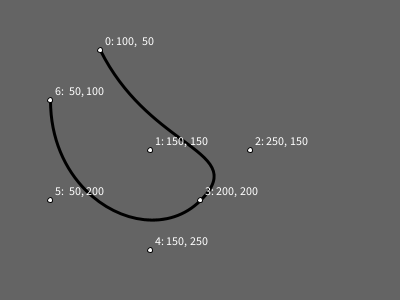
Código completo para reproduzir a imagem acima
def setup():
size(400, 300)
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
vertex(100, 50) # 0: vértice âncora
bezier_vertex(150, 150, # 1: ponto de controle
250, 150, # 2: ponto de controle
200, 200), # 3: vértice
bezier_vertex(150, 250, # 4: ponto de controle
50, 200, # 5: ponto de controle
50, 100) # 6: vértice
end_shape()
# anotações
pts = [
(100, 50), # 0
(150, 150), # 1
(250, 150), # 2
(200, 200), # 3
(150, 250), # 4
(50, 200), # 5
(50, 100), # 6
]
stroke_weight(1)
for i, (x, y) in enumerate(pts):
fill(255)
circle(x, y, 5)
text(f"{i}: {x}, {y}", x+5, y-5)
Repare neste exemplo que quando há o alinhamento entre o segundo ponto de controle de um vértice (2), o próprio vértice (3), e o primeiro ponto de controle (4), pertencente ao próximo vértice em uma sequência de vértices, haverá continuidade na curva de um trecho para outro.
Curvas Bézier quadráticas com quadratic_vertex()
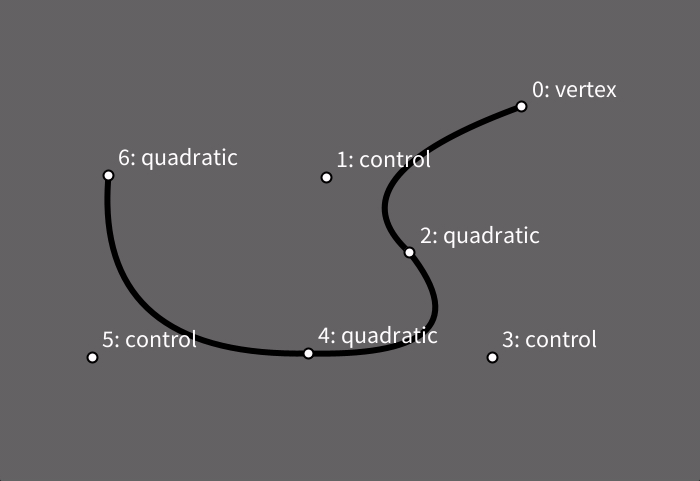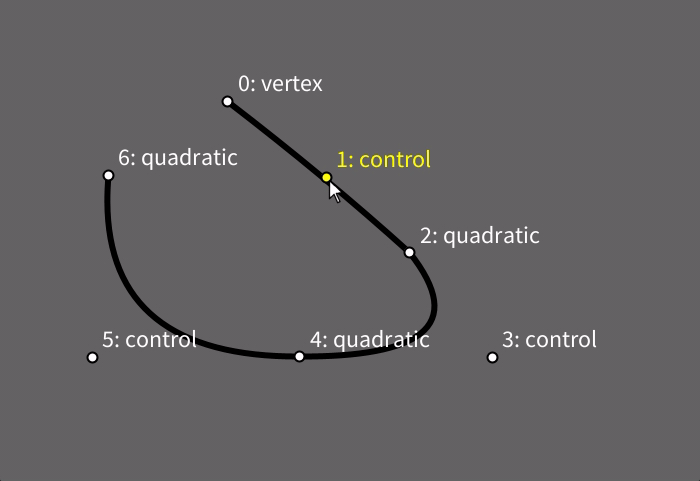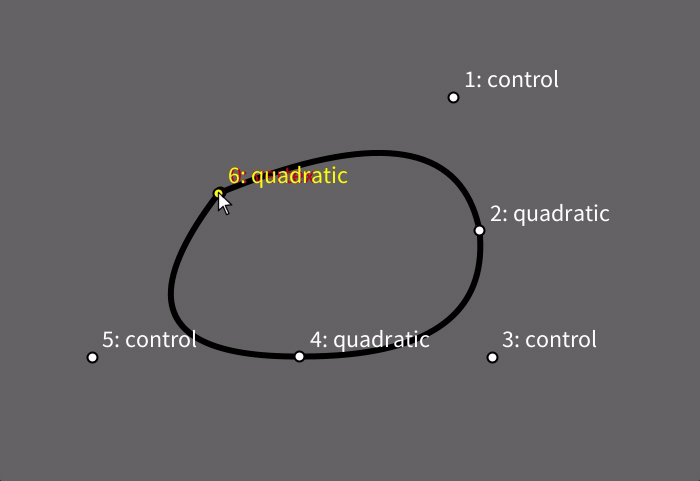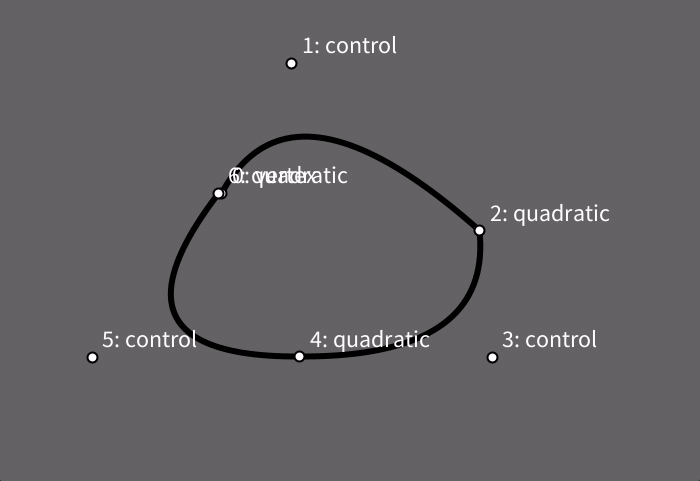
Estas curvas também são construídas dentro de um contexto begin_shape()/end_shape() e também precisam de um vértice-âncora. comummente obtido usando uma chamada da função vertex(), em seguinda, cada chamada a quadratic_vertex() inclui nos argumentos as coordenades de um ponto de controle seguidas das coordenadas do novo vértice (que por sua vez pode servir de âncora para vértices Bézier subsequentes).
size(400, 300)
begin_shape()
vertex(100, 50) # 0: vertex inicial
quadratic_vertex(150, 100, # 1: ponto de controle
250, 100) # 2: vértice-âncora
quadratic_vertex(250, 200, # 3: ponto de controle
150, 200) # 4: vértice-âncora
quadratic_vertex(50, 200, # 5: ponto de controle
50, 100) # 6: vértice-âncora final
end_shape()
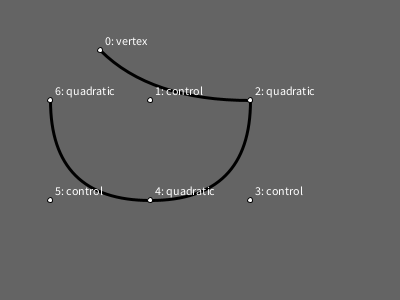
Código completo para reproduzir a imagem acima
def setup():
size(400, 300)
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
vertex(100, 50) # 0: vertex âncora inicial
quadratic_vertex(150, 100, # 1: ponto de controle
250, 100) # 2: vértice
quadratic_vertex(250, 200, # 3: ponto de controle
150, 200) # 4: vértice
quadratic_vertex(50, 200, # 5: ponto de controle
50, 100) # 6: vértice
end_shape()
pontos = [
(100, 50),
(150, 150),
(250, 100),
(250, 200),
(150, 250),
(50, 200),
(50, 100),
]
stroke_weight(1)
for i, ponto in enumerate(pontos):
x, y = ponto
fill(255)
circle(x, y, 5)
t = f'{i}: {"vertex" if i == 0 else "control" if i % 2 else "quadratic"}'
text(t, x+5, y-5)
Note como neste exemplo, na sequência final de trechos, há o alinhamento entre o ponto de controle de um vértice (3), o próprio vértice (4), e o ponto de controle (5) do próximo vértice, produzindo continuidade na curva de um trecho para outro.
Curvas Catmull-Rom com curve_vertex()
Vejamos agora as Catmull-Rom splines, uma forma de descrever curvas que não tem os pontos de controle independentes como as curvas Bézier, a curvatura em seus vértices é influenciada pelos vértices que vem antes e depois deles: é como se cada vértice fosse ao mesmo tempo sua própria âncora e ponto de controle de outros vértices anteriores e posteriores.
Vamos iterar por uma lista de coordenadas em forma de tuplas, da mesma forma que fizemos para desenhar um polígono, só que desta vez vamos experimentar usar curve_vertex() que acabamos de mencionar. Considere esta lista de pontos:
pontos = [
(100, 50),
(150, 100),
(250, 100),
(250, 200),
(150, 200),
(50, 200),
(50, 100),
]
Exemplo 1: Comportamento inesperado
Se chamarmos uma vez curve_vertex() para cada vértice dentro de um contexto de begin_shape() e end_shape(CLOSE)obteremos o seguinte resultado, esquisito (estou aqui omitindo parte do código que controla os atributos gráficos e mostra os texto com os índices dos pontos):
begin_shape()
for x, y in pontos:
curve_vertex(x, y)
end_shape(CLOSE)
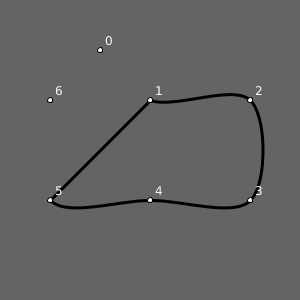
Código completo para reproduzir a imagem acima
pontos = [
(100, 50),
(150, 100),
(250, 100),
(250, 200),
(150, 200),
(50, 200),
(50, 100),
]
def setup():
size(300, 300)
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
for x, y in pontos:
curve_vertex(x, y)
end_shape(CLOSE)
stroke_weight(1)
for i, ponto in enumerate(pontos):
x, y = ponto
fill(255)
circle(x, y, 5)
text(i, x+5, y-5)
Exemplo 2: Fechando a curva corretamente
Para obter o resultado esperado (ou, caro leitor, pelo menos o que eu esperava) temos que acrescentar uma chamada com as coordenadas do último vértice antes do primeiro, e do primeiro e segundo vértices depois do último! Diga lá se não é estranho isso!
curve_vertex(pontos[-1][0], pontos[-1][1])
for x, y in pontos:
curve_vertex(x, y)
curve_vertex(pontos[0][0], pontos[0][1])
curve_vertex(pontos[1][0], pontos[1][1])
end_shape(CLOSE)
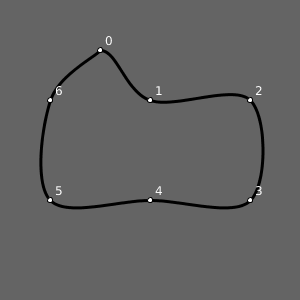
Código completo para reproduzir a imagem acima
pontos = [
(100, 50),
(150, 100),
(250, 100),
(250, 200),
(150, 200),
(50, 200),
(50, 100),
]
def setup():
size(300, 300)
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
curve_vertex(pontos[-1][0], pontos[-1][1])
for x, y in pontos:
curve_vertex(x, y)
curve_vertex(pontos[0][0], pontos[0][1])
curve_vertex(pontos[1][0], pontos[1][1])
end_shape(CLOSE)
stroke_weight(1)
for i, ponto in enumerate(pontos):
x, y=ponto
fill(255)
circle(x, y, 5)
text(i, x + 5, y - 5)
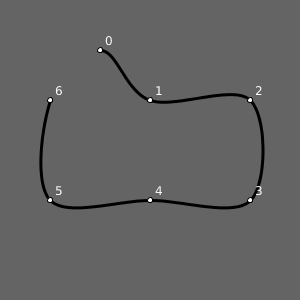
Exemplo 3: Curva aberta
É possível fazer uma curva aberta com os mesmo pontos e a mesma influência do último ponto no primeiro, e do primeiro no último, omitindo o CLOSE:
curve_vertex(pontos[-1][0], pontos[-1][1])
for x, y in pontos:
curve_vertex(x, y)
curve_vertex(pontos[0][0], pontos[0][1])
end_shape()
Código completo para reproduzir a imagem acima
pontos = [
(100, 50),
(150, 100),
(250, 100),
(250, 200),
(150, 200),
(50, 200),
(50, 100),
]
def setup():
size(300, 300)
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
curve_vertex(pontos[-1][0], pontos[-1][1])
for x, y in pontos:
curve_vertex(x, y)
curve_vertex(pontos[0][0], pontos[0][1])
curve_vertex(pontos[1][0], pontos[1][1])
pontos = [
(100, 50),
(150, 100),
(250, 100),
(250, 200),
(150, 200),
(50, 200),
(50, 100),
]
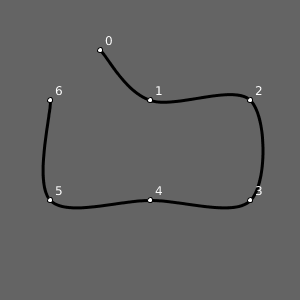
Exemplo 4: Curva aberta usando diferentes pontos
Agora se não queremos essa influência da curva fechada, é preciso repetir o primeiro e o último vértice.
begin_shape()
curve_vertex(pontos[0][0], pontos[0][1])
for x, y in pontos:
curve_vertex(x, y)
curve_vertex(pontos[-1][0], pontos[-1][1])
end_shape()
Código completo para reproduzir a imagem acima
pontos=[
(100, 50),
(150, 100),
(250, 100),
(250, 200),
(150, 200),
(50, 200),
(50, 100),
]
def setup():
size(300, 300)
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
curve_vertex(pontos[0][0], pontos[0][1])
for x, y in pontos:
curve_vertex(x, y)
curve_vertex(pontos[-1][0], pontos[-1][1])
end_shape()
stroke_weight(1)
for i, ponto in enumerate(pontos):
x, y = ponto
fill(255)
circle(x, y, 5)
text(i, x+5, y-5)
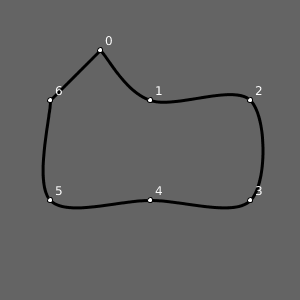
Exemplo 5: Usando end_shape(CLOSE)
Veja como ficaria acrescentando-se o CLOSE em end_shape(CLOSE). Fica um tanto estranha.
Código completo para reproduzir a imagem acima
pontos = [
(100, 50),
(150, 100),
(250, 100),
(250, 200),
(150, 200),
(50, 200),
(50, 100),
]
def setup():
size(300, 300)
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
curve_vertex(pontos[0][0], pontos[0][1])
for x, y in pontos:
curve_vertex(x, y)
curve_vertex(pontos[-1][0], pontos[-1][1])
end_shape(CLOSE)
stroke_weight(1)
for i, ponto in enumerate(pontos):
x, y=ponto
fill(255)
circle(x, y, 5)
text(i, x+5, y-5)
Extra: Um testador de curvas interativo
Desafio: Você conseguiria escrever o código que permite testar as curvas arrastando os pontos com o mouse, usando a estratégia do exemplo “arrastando vários círculos”?
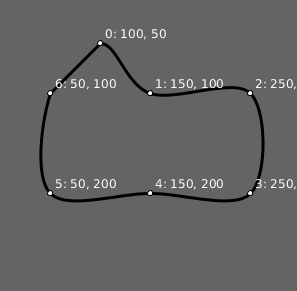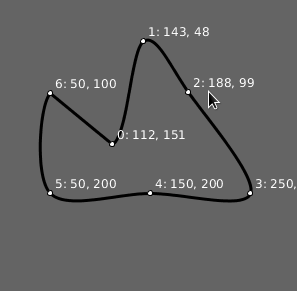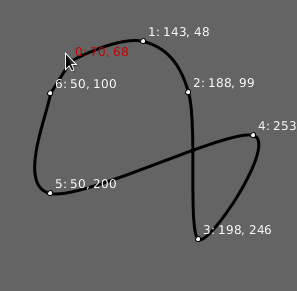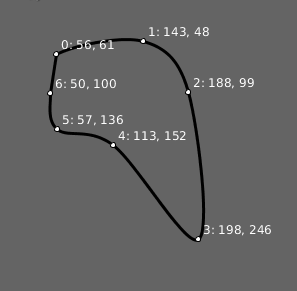
Resposta: Testador para bezier_vertex() com pontos arrastáveis. Abrir no editor online.
arrastando = None
pontos = [
(100, 50), # 0: vertex ponto âncora inicial
(150, 150), # 1: primeiro ponto de controle
(250, 150), # 2: segundo ponto de controle
(200, 200), # 3: vértice bezier
(150, 250), # 4: primeiro ponto de controle
(50, 200), # 5: segundo ponto de controle
(50, 100), # 6: vértice bezier
]
s = 2 # scale factor
def setup():
size(800, 600)
def draw():
scale(s)
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
for i, (x, y) in enumerate(pontos):
if i == 0:
vertex(x, y)
elif i % 3 == 0: # elementos divisíveis por 3 da lista
c1x, c1y = pontos[i - 2]
c2x, c2y = pontos[i - 1]
bezier_vertex(c1x, c1y, # primeiro ponto de controle
c2x, c2y, # segundo ponto de controle
x, y), # vértice
end_shape()
stroke_weight(1)
for i, ponto in enumerate(pontos):
x, y = ponto
if i == arrastando:
fill(200, 0, 0)
elif dist(mouse_x / s, mouse_y / s, x, y) < 10:
fill(255, 255, 0)
else:
fill(255)
ellipse(x, y, 5, 5)
t = f'{i}: {"vertex" if i == 0 else f"control-{i%3}" if i % 3 else "bezier"}'
text(t, x + 5, y - 5)
def mouse_pressed():
global arrastando
for i, ponto in enumerate(pontos):
x, y = ponto
if dist(mouse_x / s, mouse_y / s, x, y) < 10:
arrastando = i
break
def mouse_released():
global arrastando
arrastando = None
def mouse_dragged():
global pontos
global arrastando
if arrastando is not None:
x, y = pontos[arrastando]
x += (mouse_x - pmouse_x) / s
y += (mouse_y - pmouse_y) / s
pontos[arrastando] = x, y
Resposta: Testador para quadratic_vertex() com pontos arrastáveis. Abrir no editor online.
arrastando = None
pontos = [
(100, 50), # 0: vertex() âncora inicial
(150, 100), # 1: ponto de controle
(250, 100), # 2: vértice e âncora do próximo
(250, 200), # 3: ponto de controle
(150, 200), # 4: vértice e âncora do próximo
(50, 200), # 5: ponto de controle
(50, 100), # 6: vértice final
]
def setup():
size(400, 300)
def draw():
background(100)
stroke_weight(3)
stroke(0)
no_fill()
with begin_shape():
vertex(pontos[0][0], pontos[0][1]) # primeiro ponto (índice 0)
for (px, py), (x, y) in zip(pontos[1::2], pontos[2::2]):
# do segundo e terceiro pontos (índices 1 e 2) em diante
quadratic_vertex(px, py, x, y)
stroke_weight(1)
for i, ponto in enumerate(pontos):
x, y = ponto
if i == arrastando:
fill(200, 0, 0)
elif dist(mouse_x, mouse_y, x, y) < 10:
fill(255, 255, 0)
else:
fill(255)
ellipse(x, y, 5, 5)
t = f'{i}: {"vertex" if i == 0 else "control" if i % 2 else "quadratic"}'
text(t, x + 5, y - 5)
def mouse_pressed():
global arrastando
for i, ponto in enumerate(pontos):
x, y = ponto
if dist(mouse_x, mouse_y, x, y) < 10:
arrastando = i
break
def mouse_released():
global arrastando
arrastando = None
def mouse_dragged():
global pontos
global arrastando
if arrastando is not None:
x, y = pontos[arrastando]
x += mouse_x - pmouse_x
y += mouse_y - pmouse_y
pontos[arrastando] = x, y
Resposta: Testador para curve_vertex() com pontos arrastáveis. Abrir no editor online.
arrastando = None
pontos = [
(100, 50),
(150, 100),
(250, 100),
(250, 200),
(150, 200),
(50, 200),
(50, 100)]
def setup():
size(300, 300)
def draw():
background(100)
stroke_weight(3)
stroke(0)
no_fill()
begin_shape()
curve_vertex(pontos[-1][0], pontos[-1][1])
for x, y in pontos:
curve_vertex(x, y)
curve_vertex(pontos[0][0], pontos[0][1])
curve_vertex(pontos[1][0], pontos[1][1])
end_shape()
stroke_weight(1)
for i, ponto in enumerate(pontos):
x, y = ponto
if i == arrastando:
fill(200, 0, 0)
elif dist(mouse_x, mouse_y, x, y) < 10:
fill(255, 255, 0)
else:
fill(255)
no_stroke()
circle(x, y, 5)
t = '{}: {:03}, {:03}'.format(i, x, y)
text(t, x + 5, y - 5)
def mouse_pressed():
# quando um botão do mouse é apertado
global arrastando
for i, ponto in enumerate(pontos):
x, y = ponto
if dist(mouse_x, mouse_y, x, y) < 10:
arrastando = i
break # encerra o laço
def mouse_released():
# quando um botão do mouse é solto
global arrastando
arrastando = None
def mouse_dragged():
# quando o mouse é movido apertado
global pontos
global arrastando
if arrastando is not None:
x, y = pontos[arrastando]
x += mouse_x - pmouse_x
y += mouse_y - pmouse_y
pontos[arrastando] = x, y