Introdução à programação
com Python em um contexto visual

Transformações do sistema de coordenandas

O py5 tem funções embutidas que tornam relativamene fácil você mover, girar, crescer ou encolher objetos por meio da manipulação do sistema de coordenadas. São as funções translate(), rotate(), e scale(), apresentadas nesta págima. Também serão apresentadas as funções, de grande importância, que permitem ‘guardar’ e ‘devolver’ o estado anterior do sistema de coordenadas, são elas: push_matrix() e pop_matrix().

Essas funções mencionadas, em conjunto, tornam possível, entre outras coisas, desenhar um retângulo inclinado na tela. Note que até agoras, usando apenas a função rect(), só podemos desenhar retângulos com os lados alinhados ao sistema de coordenadas. Uma forma possível de se desenhar um retângulo inclinado é elencar as coordenadas dos vértices do retângulo e calcular a posição girada de cada um deles, usando seno e cosseno, para por fim desenhar um polígono com as novas posições usando begin_shape(), vertex() e end_shape(), o que pode ser interessante também, mas costuma ser mais trabalhoso.

Começando com a rotação, para ver como as coisas são estranhas

Suponha que queremos desenhar um quadrado no centro da tela, inclinado em 10 graus. Vejamos o que acontece quando usamos a função rotate() que gira o sistema de coordenadas.

Para termos um elemento inicial de comparação, vamos primeiro desenhar um quadrado sem girar, usando as coordendadas da metade da largura e da altura da área de desenho (vamos chamar este de “quadrado 0”).

Então, vamos usar a função rotate(), e em seguida vamos desenhar um quadrado com os mesmos argumentos novamente (“quadrado 1”). Por fim, vamos repetir tanto a rotação como o a chamada de função que desenha o quadrado mais uma vez (“quadrado 2”).

Nota: No py5 quando uma função pede um ângulo como argumento, espera que você informe esse ângulo em radianos, por isso, se você pensa em graus, use radians(angulo_em_graus) para converter.

def setup():
    size(500, 500)
    rect_mode(CENTER)
    no_fill()
    square(250, 250, 200)  # quadrado 0
    rotate(radians(10))
    square(250, 250, 200)  # quadrado 1
    rotate(radians(10))
    square(250, 250, 200)  # quadrado 2

O resultado é o seguinte.

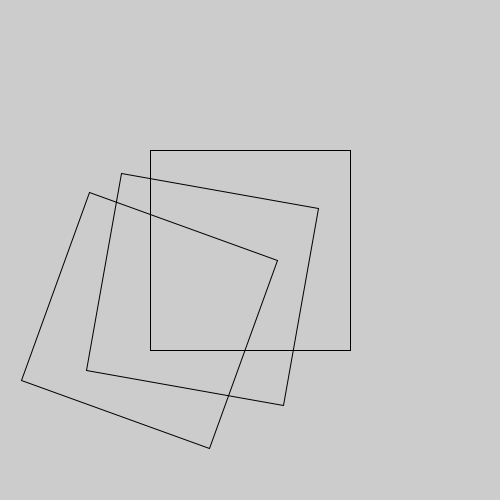
Você percebe o que está acontecendo? Pense nestas questões:

As respostas para essas perguntas são:

Resolvendo a primeira parte, a escolha do centro da rotação, usando a translação

Se movermos a origem para o ponto no centro da área de desenho, usando translate(), com os argumentos 250, 250, conseguiremos girar o sitema de coordenadas em torno de um novo centro.

def setup():
    size(500, 500)
    rect_mode(CENTER)
    no_fill()
    square(250, 250, 200)
    translate(250, 250)
    rotate(radians(10))
    square(0, 0, 200)
    rotate(radians(10))
    square(0, 0, 200)

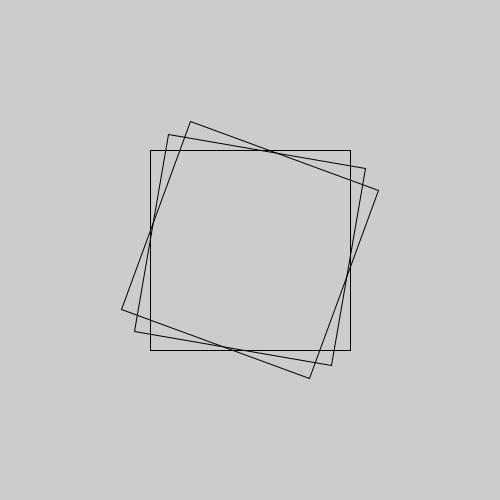
Note que o segundo e terceiro quadrados são desenhados com square(0, 0, 200), nas novas coordenadas do centro da tela após o translate(250, 250), e não mais em square(250, 250, 200).

A questão da acumulação de translate() e rotate()

A segunda parte do problema, que se manifestou sutilmente até agora, é de que as transformações do sistema de coordenadas não cumulativas. Como mover e girar o mesmo papel milimetrado sucessivamente.

Suponha que queremos desenhar uma fila de quadrados girados, e veja este exemplo ingênuo de uma função quadrado_girado_errado() que desenha, bem, um quadrado girado. O código a seguir, usando a função quadrado_girado_errado() falha horrívelmente na missão de desenhar uma fila com os quadrados alinhados com Y valendo 100, como parecem indicar as coordenadas passadas como argumentos (100, 100), (250, 100) e (400, 100).

def setup():
    size(500, 500)
    rect_mode(CENTER)
    no_fill()

def quadrado_girado_errado(x, y, lado, rot):
    translate(x, y)
    rotate(rot)
    square(0, 0, lado)
    
def draw():
    background(200)
    quadrado_girado_errado(100, 100, 100, radians(10))
    quadrado_girado_errado(250, 100, 100, radians(10))
    quadrado_girado_errado(400, 100, 100, radians(10))

Cada chamada a função quadrado_girado_errado() empurra a origem do sistema de coordenadas mais um pouco, e também gira 10 graus, então o segundo quadrado girado cai mais longe e mais girado, o terceiro já fica para fora da tela, mais abaixo à direita!

A solução com push_matrix e pop_matrix

É possível fazer uma espécie “backup” do atual sistema de coordenadas, usando a função push_matrix() depois de feito o desenho que precisamos com as coordenadas alteradas, pop_matrix() devolve ao sketch o estado anterior do sistema de coordenadas. Com esta versão modificada da função quadrado_girado() conseguimos posicionar à vontade nossos quadrados girados.

def quadrado_girado(x, y, lado, rot):
    push_matrix()  # guarda a matriz atual do sistema de coordenadas
    translate(x, y)
    rotate(rot)
    square(0, 0, lado)
    pop_matrix()  # recupera a matriz do sistema de coordenadas anterior

Um exemplo de uso do quadrado girado

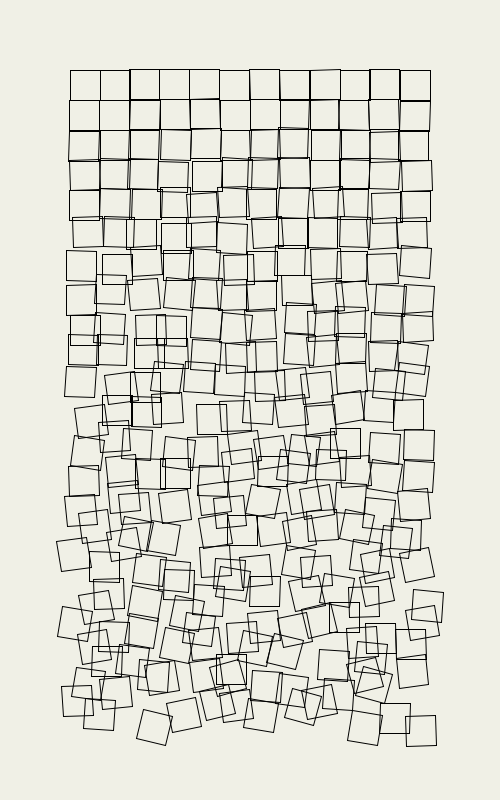
O artista pioneiro da arte computacional Georg Nees tem uma obra “Schotter” (1968-1970), cujas formas podemos tentar recriar com os quadrados girados e um aumento gradual de deslocamentos e rotações usando random().

Schotter

colunas = 12
filas = 22
tam = 30  # tamanho dos quadrados

def setup():
    size(500, 800)
    rect_mode(CENTER)
    no_loop() # desativa a repetição do draw
    no_fill()
     
def draw():
    background(240, 240, 230)
    largura_grade = tam * colunas
    altura_grade = tam * filas
    margem = (width - largura_grade) / 2
    margem_vertical = (height - altura_grade) / 2
    desordem = 0
    for fila in range(filas):
        y = margem_vertical + fila * tam + tam / 2         
        for col in range(colunas):
            x = margem + col * tam + tam / 2
            dx = random(-desordem / 16, desordem / 16)  # deslocamento x
            dy = random(-desordem / 16, desordem / 16)  # deslocamento y
            ar = random(-desordem / 16, desordem / 16)  # rotação em graus
            quadrado_girado(x + dx, y + dy, tam, radians(ar))
            desordem = desordem + 1
        
def quadrado_girado(x, y, lado, rot):
    push_matrix()  # preserva do sistema de coordenadas
    translate(x, y)
    rotate(rot)
    square(0, 0, lado)
    pop_matrix()  # restaura o sistema de coordenadas
    
def key_pressed():
    save_frame('###.png')
    redraw()

Mudando a escala

Além da translação e rotação é possível também escalar o sistema de coordenada com scale() e entortar com shear_x() e shear_y(). São transformações um pouco mais difíceis de imaginar com a metáfora do papel milimetrado, que precisaria ser de uma borracha mágica, mas, vejamos um exemplo curto só com a transformação da mudança de escala.

def setup():
    size(500, 500)
    rect_mode(CENTER)
    no_fill()
    no_loop()
    square(100, 100, 50)
    scale(1.5)
    square(100, 100, 50)
    scale(1.5)
    square(100, 100, 50)
    scale(1.5)
    square(100, 100, 50)
    scale(1.5)

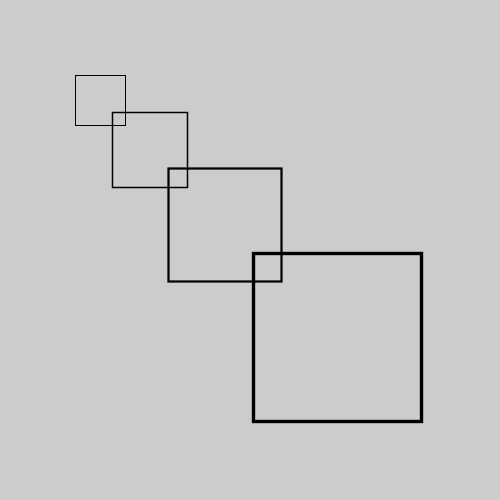
Repare no exemplo acima como a aplicação do fator de escala acontece baseada na origem do sistema de coordanadas, que não foi modificada, e a transformação de escala é cumulativa. Note também como a escala afeta a espessura de linha do traço, o atributo gráfico que pode ser controlado com stroke_weight().

Você consegue imaginar qual o código que gera a imagem a seguir?

Pense em como você escreveria o código e depois clique para a resposta 
def setup():
    size(500, 500)
    rect_mode(CENTER)
    no_fill()
    no_loop()
    translate(250, 250)
    square(0, 0, 50)
    scale(1.5)
    square(0, 0, 50)
    scale(1.5)
    square(0, 0, 50)
    scale(1.5)
    square(0, 0, 50)
    scale(1.5)

A matriz de transformação e a origem de push_matrix e pop_matrix

Na matemática temos a ideia de matriz, que são objetos formados por linhas e colunas de números. Sempre que você faz uma rotação, translação ou mudança de escala, as informações necessárias para essa transformação são armazenadas em uma matriz de 3 colunas e duas linhas, e é por isso que as funções push_matrix() e pop_matrix() têm essa palavra matrix no nome.

Você não precisa interagir diretamante com essa “matriz de transformações” se não quiser, mas por curiosidade veja o exemplo abaixo que exibe os valores dela com print_matrix().

def setup():
    size(500, 500)
    print('estado inicial')
    print_matrix()
    translate(250, 250)
    print('depois de translate(250, 250)')
    print_matrix()
    rotate(radians(10))        
    print('depois de rotate(radians(10))')
    print_matrix()

O resultado no console:

estado inicial
 1.0000  0.0000  0.0000
 0.0000  1.0000  0.0000
depois de translate(250, 250)
 001.0000  000.0000  250.0000
 000.0000  001.0000  250.0000
depois de rotate(radians(10))
 000.9848 -000.1736  250.0000
 000.1736  000.9848  250.0000

Já a parte push e pop dos nomes vêm de uma estrutura de dados muito comum na computação conhecida como pilha (stack). Imagine uma pilha de livros, e considere que se você acrescenta um livro na pilha ele vai por cima, e se acrescentar mais um ele vai por cima do anterior. Já na hora de tirar livros o mais natural é remover o mais de cima antes do seguinte, e assim por diante.

Tradicionalmente, adicionamos itens em uma pilha com instruções nomeadas push e removemos com instruções nomeadas pop. A influência dessa nomenclatura é tão grande que, no Python, usamos .pop() para acessar e remover o último item de uma lista, e, no JavaScript, .push() é usado para acrescentar itens em um array (semelhante ao .append() para listas no Python).

De maneira parecida então, push_matrix() coloca a descrição do estado atual do sistema de coordenadas no topo de uma pilha na memória, e pop_matrix() remove e restaura a última descrição de estado da pilha.

Uma forma alternativa de uso do push_matrix

No py5 é possível usar a sintaxe do que chamamos “gerenciadores de contexto”, a linha with push_matrix(): indica o início de um bloco de código onde vai acontecer uma transformação do sistema de coordenadas, e quando a indentação acaba, acontece um pop_matrix() “automático”.

def quadrado_girado(x, y, lado, rot):
    with push_matrix():
        translate(x, y)
        rotate(rot)
        square(0, 0, lado)

Algumas dicas importantes

Transformações tridimensionais

Se você estiver trabalhando em três dimensões, poderá chamar a função translate() com três argumentos para as distâncias x, y, e z, a função scale() pode ser chamada também com três argumentos e as funções rotate_x(), rotate_y() e rotate_z(), que recebem um argumento em radianos e fazem a rotação em torno de cada eixo. Vej o código que produz esta imagem na página sobre desenho em 3D.

Assuntos relacionados