Um pouco de ângulos, com seno, cosseno e arco tangente
As funções sin(), cos() e atan2() do py5
As funções trigonométricas não são nenhum bicho de sete cabeças, 2π cabeças, no máximo…
Para começar é preciso saber que quando uma dessas funções, como sin(ang)(seno) e cos(ang) (cosseno) pede um ângulo como argumento (o valor entre parênteses), espera que você informe esse ângulo em radianos, um jeito de descrever ângulos em que 2π (duas vezes pi radianos) significa 360° (360 graus), π radianos é 180°, π/2 é 90° e assim por diante. Para facilitar, o Processing oferece várias constantes relacionadas: TWO_PI (ou TAU, 360°), PI (180°), HALF_PI (90°), QUARTER_PI (45°).
Se você pensa em graus, e não se sente confortável usando ângulos em radianos, pode usar radians(angulo_em_graus) para converter graus em radianos. Outras funções, como atan2(), que vamos ver nesta página, devolvem como resultado um ângulo em radianos, que por sua vez pode ser convertido em graus com degrees(angulo_em_radianos) se você precisar.
Seno e cosseno
Na origem essas funções tratam das relações entre ângulos e proporções das medidas dos triângulos, sendo muito estudadas, demonstradas, em triângulos retângulos ou em um círculo de raio unitário(o ciclo trigronométrico), mas para além desse contexto, das coisas mais úteis que você pode querer saber, e acredito não ser difícil demonstrar aqui, é que essas funções devolvem valores entre -1 e 1 de maneira cíclica, periódica.
Os primeiros exemplos a seguir são para visualizar como se dá o comportamento do seno e do cosseno.
sin() e cos() no espaço
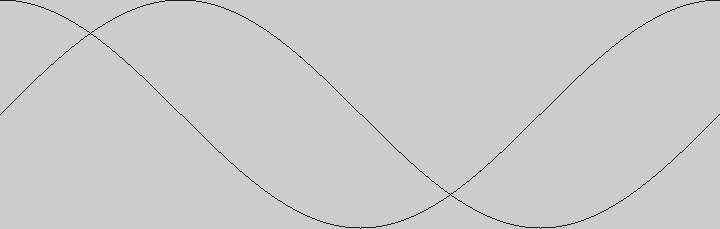
Para produzir a imagem acima, criamos um laço repetição que produz um x de 0 a 720 , convertemos esse xnum ângulo em radianos e dividimos por 2, de forma a obter ângulos de 0 a 2π radianos (ou 0° a 360°).
Vamos multiplicar o valor do seno e do cosseno do ângulo pela metade da altura da tela (aproveitando para inverter o sinal pois o eixo Y do Processing cresce para baixo e estamos acostumados a ver os gráficos com a parte positiva para cima). Para deslocar a origem para baixo somamos esse mesmo valor de metade da altura da tela.
size(720, 229) # 360×2, 4 radianos
for x in range(width):
meia_altura = height / 2
ang = radians(x / 2.0) # 720 pixels -> 360 graus
seno = sin(ang) * -meia_altura + meia_altura
point(x, seno)
cosseno = cos(ang) * -meia_altura + meia_altura
point(x, cosseno)
Qual é o seno e qual o cosseno? Veja o resultado das instruções a seguir.
print(sin(0)) # exibe no console: 0.0
print(cos(0)) # exibe no console: 1.0
O seno é o que começa à esquerda no 0, na meia altura da tela, e o cosseno é o que começa no alto valendo 1.
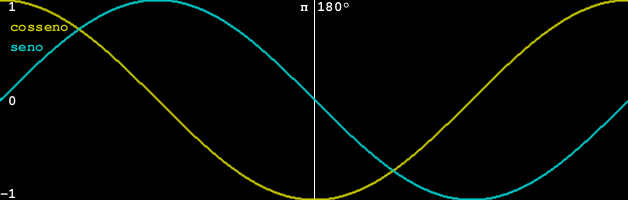
Outra versão com algumas indicações
Desta vez o exemplo usa translate() e scale() para deslocar e inverter o eixo Y. E o X vai de 0 a aproximadamente 2π mutiplicado por 100
def setup():
size(628, 200) # malandrangem 2π×100, 2×100
textFont(createFont('FreeMono Bold', 14))
background(0)
translate(0, 100) # desloca o Y meia tela
indicacoes() # desenha textos e linha em π
strokeWeight(2)
scale(1, -1) # inverte o Y
for x in range(width):
a = x / 100.0 # width ~2π×100
y_cosseno = cos(a) * 100
stroke(200, 200, 0)
point(x, y_cosseno)
y_seno = sin(a) * 100
stroke(0, 200, 200)
point(x, y_seno)
def indicacoes():
fill(255)
text(" 0", 0, 5)
text("-1", 0, 98)
text(" 1", 0, -90)
stroke(255)
strokeWeight(1)
line(width / 2.0, -height / 2.0,
width / 2.0, height / 2.0)
text(u"π 180°", -14 + width / 2.0,
10 - height / 2.0)
fill(200, 200, 0)
text("cosseno", 10, -70)
fill(0, 200, 200)
text("seno", 10, -50)
sin() e cos() no tempo
Seno e cosseno são muito úteis para fazer animações cíclicas, é muito fácil usar a contagem pronta dos quadros oferecida pelo Processing, frameCount como se fosse um ângulo em graus, converta em radianos e voi-lá!

def setup():
size(628, 200) # malandrangem 2π×100, 200
textFont(createFont('FreeMono Bold', 14))
def draw():
background(0)
a = radians(frameCount)
indicacoes() # desenha textos e linha móvel
tam_cosseno = 100 + cos(a) * 100
fill(200, 200, 0)
ellipse(width / 3, height / 2,
tam_cosseno, tam_cosseno)
tam_seno = 100 + sin(a) * 100
fill(0, 200, 200)
ellipse(2 * width / 3, height / 2,
tam_seno, tam_seno)
def indicacoes():
a = frameCount % 360
x = radians(a) * 100 # width tem aprox. 2π×100 pixels
stroke(255)
line(x, 0, x, height)
fill(255)
noStroke()
text(u'ângulo: {:0>3}'.format(a), 10, 20)
fill(200, 200, 0)
text("cosseno", 10, 40)
fill(0, 200, 200)
text("seno", 10, 60)
Note que seno ou cosseno valendo zero significa que a bolinha fica com tamanho 100, com valor -1 ela deseaparece e com o valor 1 ela ganha o seu diâmetro máximo de 200 pixels.
Seno e cosseno fornecem as coordenadas dos pontos de um círculo!
Com seno, cosseno, o raio e coordenadas do centro, é possível calcular o X e Y de um ponto para cada ângulo em um círculo, isso permite desenhar polígonos regulares e estrelas, por exemplo.

size(400, 400)
x_centro, y_centro = width / 2, height / 2
raio = 180
for graus in range(0, 360, 18): # cada 18°
ang = radians(graus)
x = x_centro + raio * cos(ang)
y = y_centro + raio * sin(ang)
strokeWeight(5)
point(x, y)
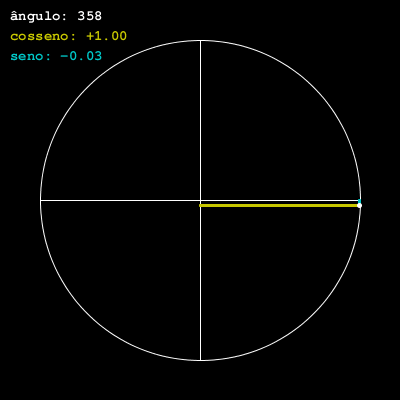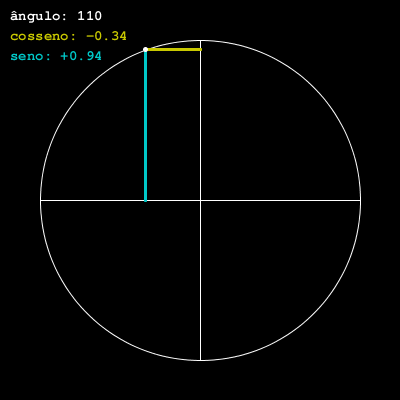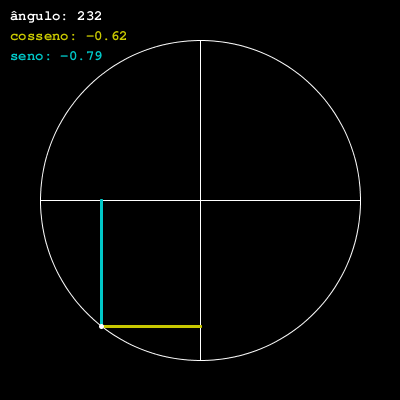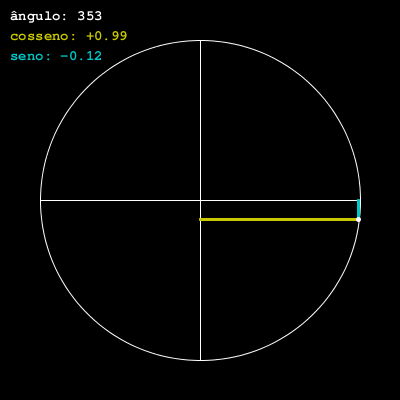
Uma versão animada e com algumas indicações
Vamos agora desenhar atualizando o ângulo com o tempo, dessa forma animando o ponto no círculo.
def setup():
global x_centro, y_centro, raio
size(400, 400)
textFont(createFont('FreeMono Bold', 14))
x_centro, y_centro = width / 2, height / 2
raio = 160
def draw():
background(0)
indicacoes() # desenha textos, círculo e linhas
ang = -radians(frameCount) # prefiro anti-horário
x = x_centro + raio * cos(ang)
y = y_centro + raio * sin(ang)
strokeWeight(3)
stroke(0, 200, 200)
line(x, y_centro, x, y) # linha do seno
stroke(200, 200, 0)
line(x_centro, y, x, y) # linha do cosseno
strokeWeight(5)
stroke(255)
point(x, y) # o ponto no círculo
def indicacoes():
stroke(255)
strokeWeight(1)
noFill()
circle(x_centro, y_centro, raio * 2)
line(x_centro, y_centro - raio,
x_centro, y_centro + raio)
line(x_centro - raio, y_centro,
x_centro + raio, y_centro)
fill(255)
graus = frameCount % 360
ang = radians(graus)
seno = sin(ang)
cosseno = cos(ang)
text(u'ângulo: {:0>3}'.format(graus), 10, 20)
fill(200, 200, 0)
text("cosseno: {:+.2f}".format(cosseno), 10, 40)
fill(0, 200, 200)
text("seno: {:+.2f}".format(seno), 10, 60)
A função do arco tangente
Como descobrir a inclinação de um segmento de reta?
A função atan() (arco tangente) devolve o ângulo a partir da tangente desse ângulo, e é possível calcular a tangente dividindo o cateto oposto pelo cateto adjacente, no caso os lados paralelos aos eixos, do triângulo formado pelos pontos de uma ‘linha’ (como chamamos informalmente um segmento de reta definido por dois pontos).
O cateto oposto é a diferença dos valores de Y e o adjacente a diferença dos valores de X das coordenadas da linha. Só que na prática isso é uma encrenca, se a linha ficar na vertical teremos uma divisão por zero… Muito mais prático é entregar o trabalho de dividir para uma ‘versão 2’ da função do arco tangente: atan2(dy, dx), os dois argumentos são as medidas dos catetos e ela cuida de tudo nos devolvendo um ângulo em radianos.
Note que vamos obter ângulos com valores entre -π e π (entre -180 e 180 graus) em vez de 0 a 2π. Você pode somar a constate PI do Processing ao valor se preferir essa segunda faixa.
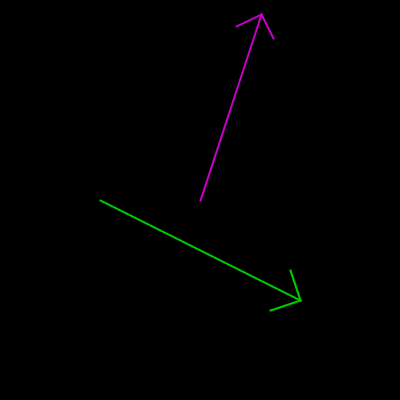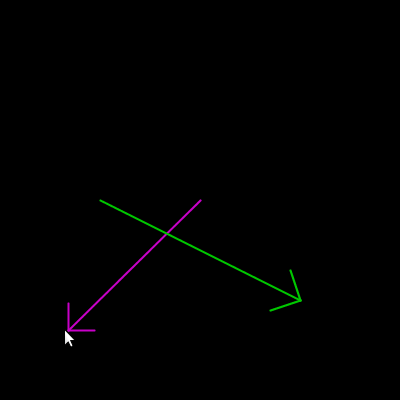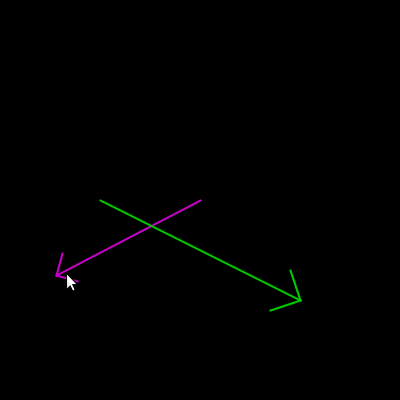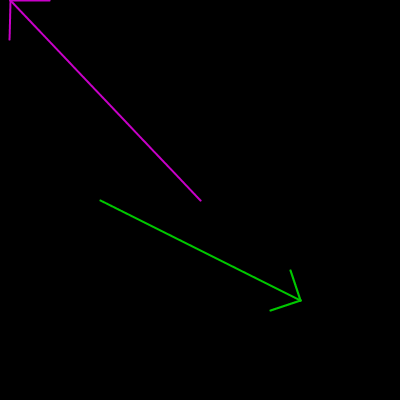
Desenhando uma seta com atan2()
Para demonstrar a utilidade de se saber o ângulo de uma linha, vamos desenhar uma seta! Na verdade, saber o ângulo de uma linha da qual conhecemos as coordenadas permite desenhar todo tipo de elemento alinhado ou com ângulo a ela relacionado.
A estratégia mostrada inicialmente é usar o ângulo da linha para girar o sistema de coordenadas, dentro da função seta(), e desenhar a cabeça com as coordenadas transformadas.
def setup():
size(400, 400)
strokeWeight(2)
def draw():
background(0)
stroke(200, 0, 200)
seta(200, 200, mouseX, mouseY)
stroke(0, 200, 0)
seta(100, 200, 300, 300)
def seta(xa, ya, xb, yb):
tam_seta = dist(xa, ya, xb, yb)
ang = atan2(yb - ya, xb - xa)
line(xa, ya, xb, yb)
pushMatrix()
translate(xb, yb)
rotate(ang)
tam_ponta = tam_seta / 10
line(0, 0, -tam_ponta, tam_ponta)
line(0, 0, -tam_ponta, -tam_ponta)
popMatrix()
Mas, você pode querer calcular você mesma as coordenadas dos vértices da cabeça da seta assim:
def seta(xa, ya, xb, yb):
tam_seta = dist(xa, ya, xb, yb)
ang = atan2(yb - ya, xb - xa)
line(xa, ya, xb, yb)
tam_ponta = tam_seta / 10 * sqrt(2)
xpe = xb + cos(ang + QUARTER_PI + PI) * tam_ponta
ype = yb + sin(ang + QUARTER_PI + PI) * tam_ponta
line(xb, yb, xpe, ype) # parte esquerda da ponta
xpd = xb + cos(ang - QUARTER_PI + PI) * tam_ponta
ypd = yb + sin(ang - QUARTER_PI + PI) * tam_ponta
line(xb, yb, xpd, ypd) # parte direita da ponta
Apontando para o mouse
Ampliando a estratégia mostrada na segunda versão da seta, em que a coordenada dos pontos são calculados usando seno e cosseno, é possível fazer setas de tamanho fixo, apontadas para o mouse. O ângulo continua sendo providenciado pela função do arco tangente.
def setup():
size(400, 400)
strokeWeight(2)
noCursor() # desativa a setinha do mouse
def draw():
background(200)
for i in range(10):
x = 20 + i * 40
for j in range(10):
y = 20 + j * 40
if dist(x, y, mouseX, mouseY) > 35:
seta_tam_fixo(x, y, mouseX, mouseY, 35)
def seta_tam_fixo(xa, ya, xb, yb, tam):
ang = atan2(yb - ya, xb - xa)
tam_ponta = tam / 4 * sqrt(2)
xp = xa + cos(ang) * tam
yp = ya + sin(ang) * tam
line(xa, ya, xp, yp) # corpo com tamanho fixo
xpe = xp + cos(ang + QUARTER_PI + PI) * tam_ponta
ype = yp + sin(ang + QUARTER_PI + PI) * tam_ponta
line(xp, yp, xpe, ype) # parte esquerda da ponta
xpd = xp + cos(ang - QUARTER_PI + PI) * tam_ponta
ypd = yp + sin(ang - QUARTER_PI + PI) * tam_ponta
line(xp, yp, xpd, ypd) # parte direita da ponta

Note que ocultei a setinha do mouse com noCursor(), é possível voltar com o cursor, e escolher outros formatos ou até uma imagem como cursor, consulte a documentação de cursor().