Operações com vetores e a classe Py5Vector
Vetores no fundo são sequências de números, imagine os números aqui representados como listas: [105, 42] ou [120, 81, 35]. Os números que formam um vetor são chamados componentes e os vetores, em teoria, podem ter o número de componentes que você quiser, mas nos interessam mais neste momento os vetores com 2 ou 3 componentes pois eles são úteis para representar coordenadas, velocidades e acelerações em duas e três dimensões. Podemos visualizá-los como pontos ou como segmentos de reta orientados, a representação gráfica usual é como uma seta.
É possível trabalhar com vetores de muito mais dimensôes, que não são fáceis de visualizar, muito usados em computação científica, da álgebra linear à representação de palavras para processamento de linguagem natural e tradução automatizada.
Em vez de listas com números, os componentes, vamos usar objetos da classe Py5Vector. É possível somar e subtrair vetores somando os componentes de cada um nas mesmas posições, é fácil também multiplicar ou dividir um vetor por um número comum, multiplicando cada componente pelo número (e isso multiplica ou divide a magnitude do vetor). Já para multiplicar vetores entre si tem mais de uma maneira de fazer, o chamado produto escalar(dot product) e o produto vetorial(cross product). Mas podemos pedir para o computador fazer para nós essas operações!
Py5Vector2D
Vetores 2-D, 3-D e 4-D, de duas, três e quatro dimensões, podem ser expressos no py5 como objetos da classe Py5Vector. Vamos começar explorando os de duas dimesões, construídos com Py5Vector(x, y). Acredito que em breve você vai concordar comigo que essa classe vai facilitar muito fazer operações, contas e transformações, com vetores, o que é especialmente útil para animar partículas e calcular diversas geometrias.
pos = Py5Vector(75, 400) # posição inicial
vel = Py5Vector(2, -8) # velocidade inicial
acel = Py5Vector(0, 0.1) # aceleração, para baixo
def setup():
size(500, 500)
stroke_weight(5)
def draw():
global pos, vel
point(pos.x, pos.y)
pos += vel
vel += acel
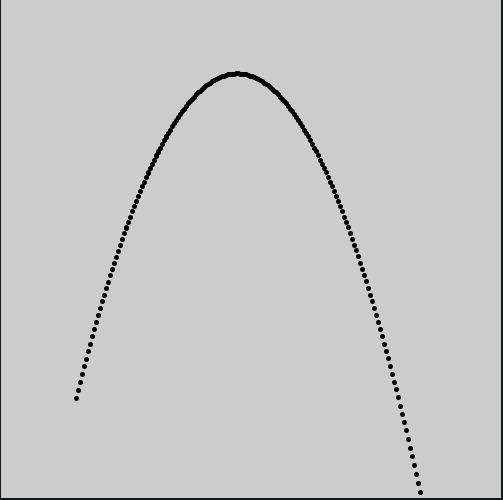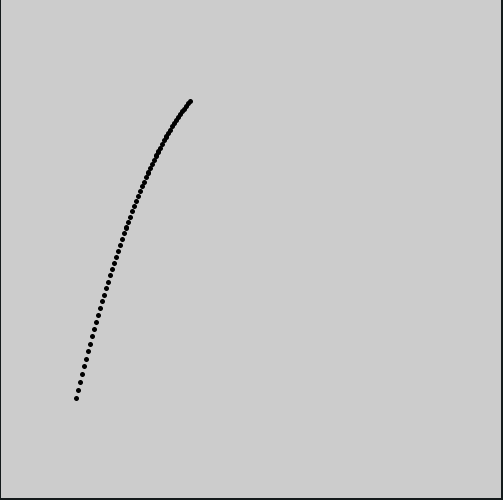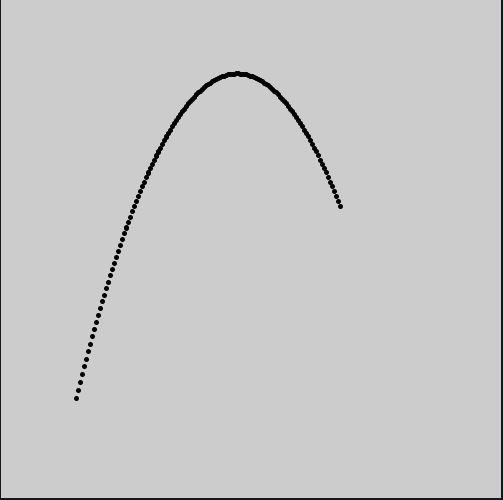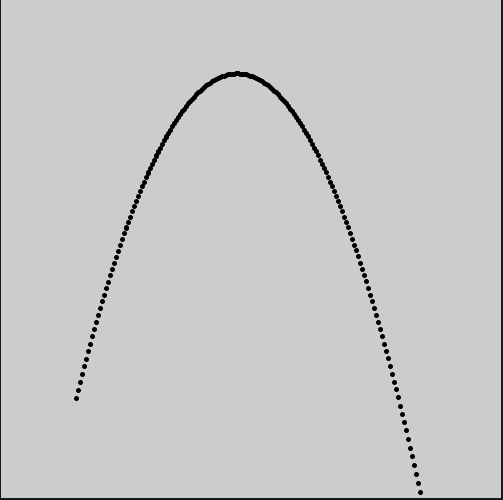
No exemplo acima, o vetor pos representa a posição de uma partícula, o vetor vel a sua velociade, e o vetor acel uma aceleração para baixo(que pode ser interpretada como resultado de uma força causada pela ação da gravidade, por exemplo).
No código o operador de atribuição aumentada +=, aplicado à variável global pos, faz a velocidade alterar a posição, algo equivalente a pos = pos + vel, e da mesma maneira a velocidade é alterada pela aceleração acel.
Uma classe de partículas que fogem do mouse
particles = []
def setup():
size(400, 400)
stroke_weight(5)
for i in range(200):
particles.append(Particle(random(width), random(height)))
def draw():
background(200)
mouse_pos = Py5Vector(mouse_x, mouse_y)
for p in particles:
p.update(mouse_pos)
class Particle:
def __init__(self, x, y):
self.pos = Py5Vector(x, y)
self.vel = Py5Vector(0, 0) # PVector.random2D()
def update(self, mouse_pos):
delta = self.pos - mouse_pos
d = delta.mag
if 0 < d < 50:
acel = delta.norm * 0.01
self.vel += acel
self.pos += self.vel
self.vel = self.vel * 0.995 # slow down
stroke(max(0, 255 - d * 5,), 0, 0)
point(self.pos.x, self.pos.y)
if self.pos.x < 0:
self.pos.x = width
elif self.pos.x > width:
self.pos.x = 0
if self.pos.y < 0:
self.pos.y = height
elif self.pos.y > height:
self.pos.y = 0

Neste segundo exemplo a diferença (subtração) entre um vetor criado com as cordenadas da posição do mouse (mouse_pos) e o vetor que representa a posição de cada partícula (self.pos) é usada para calcular um vetor delta cuja magnitude delta.mag afeta a aceleração das partículas.
Note como delta é usado para calcular a direção da aceleração. O código poderia talvez ser mais eficiente usando o quadrado da magnitude (.mag_sq) que é mais econômico que o cálculo da magnitude. Foi usada a propriedade .norm, para obter um vetor “normalizado” ou unitário (de magnitude 1) que mantém apenas a direção do vetor original, também poderíamos usar o método .normalize().
Métodos e propriedades dos vetores Py5Vector
| método / campo | descrição |
|---|---|
| random(dim=2) | Cria um novo vetor unitário 2D com uma direção aleatória. |
| random(dim=3) | Cria um novo vetor unitário 3D com uma direção aleatória. |
| from_heading() | Cria um novo vetor unitário 2D a partir de um ângulo. |
| copy | Produz um novo vetor, cópia do original. |
| data | O array Numpy usado para guardar os valores do vetor. |
| dim | Informa as dimensões do do vetor (2, 3, ou 4). |
| mag | Calcula a magnitude do vetor. |
| mag_sq | Calcula a magnitude ao quadrado do vetor. É mais rápido que calcular a magnitude! |
| dist() | Calcula a distância entre dois pontos representados por dois vetores. |
| dot() | Calcula o produto escalar(dot product) entre dois vetores. |
| cross() | Calcula o produto vetorial(cross product) entre dois vetores. |
| from_heading() | Cria vetor a partir de uma direção, ângulo em radianos. |
| normalize() | Normaliza o vetor, isto é faz com que fique com a magnitude 1, mantendo a mesma direção. |
| norm | Cópia “normalizada”, com magnitude 1, do vetor, mantendo a direção. |
| set_mag() | Define, isto é, altera, a magnitude do vetor. |
| heading | O ângulo de rotação do vetor, isto é, para onde ele aponta. |
| rotate() | Gira o vetor um certo ângulo em radianos (funciona apenas com vetores 2D e 3D). |
| lerp() | Produz o resultado da interpolação linear entre dois vetores. |
| angle_between() | Calcula o ângulo entre dois vetores. |